计算机二级C++

数据结构

逻辑结构

  • 集合：数据结构中的元素除了“同属一个集合”的相互关系外，别无其他关系。
  • 线性结构：元素存在的一对一关系。
  • 树形结构：元素存在的一对多的关系
  • 图形结构：元素存在多对多的关系。

存储结构

  • 顺序存储：把逻辑上相邻的结点存储在物理位置相邻的存储单元里，结点间的逻辑关系由存储单元的邻接关系来体现，即用存储关系表示逻辑关系
  • 链接存储：逻辑是相邻的结点在物理上并不一定相邻，结点间的逻辑关系由附加的指针域表示，即用附加的指针表示逻辑关系
  • 索引存储：除建立存储结点信息外，还建立附加的索引表来标识结点的地址，即用附加的的索引表表示逻辑关系

数据结点的运算

域数据的逻辑结构相对应的运算集合，主要包括输入，输出，查找，排序，插入，删除及更新等。

数据结构的分类

逻辑结构分为线性结构和非线性结构。

1.线性结构：线性表，栈，队列。

2.非线性结构：树，二叉树，图。

  • 链表的类型：

    ​ 单链表：只有一个指针

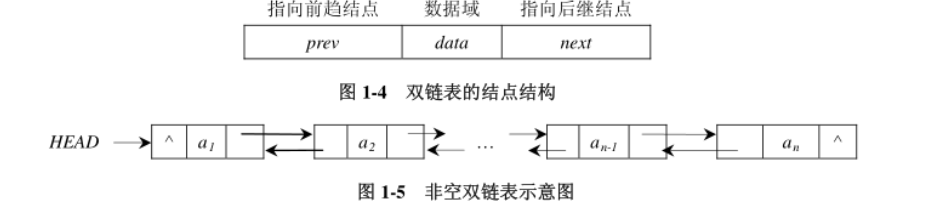
​ 双向链表：每个结点的指针域包括两个指针，一个只向前趋结点，另一个指向其后继结点

​ 循环链表：最后一个结点的指针域不为空，而是指向表头结点

  • 链表的运算

    1.基本运算：

    ​ 插入结点：不需要移动数据元素，只需要修改相关结点指针，不会出现“上溢”现象。

    ​ 删除结点：不需要移动数据元素，只需要修改相关结点指针。

    2.双链表的运算：

    ​ 双链表的运算域单链表相比，每次运算都要修改指针域中两个指针的值；同时，双链表允许从后向前运算。

    3.循环链表的运算

    ​ 为了实空表与非空表运算的统一，循环链表中增加了一个表头结点（不是第一个数据元素），其指针指向第一个数据元素，二循环链表的头指针指向表头结点。循环链表的优点主要体现在两个方面：只要指出表中任何一个结点的位置，就可以从它出发访问到表中其他的所有结点；任何情况下，循环链表中至少有一个结点。

栈与队列

栈的概念

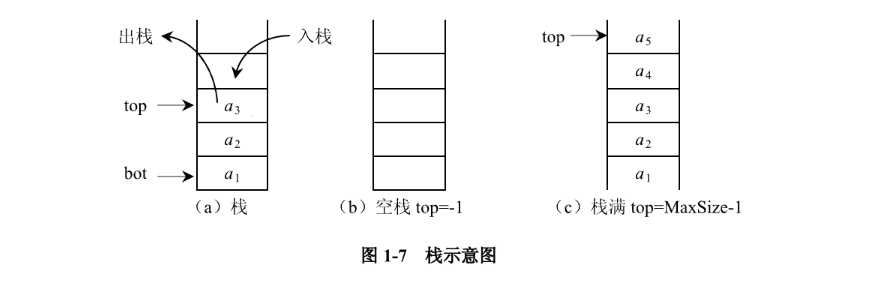
栈是限定在一端进行插入与删除运算的线性表。栈的存储结构与线性表类似，包括顺序栈和链式栈。对于顺序栈Stack，设其空间大小（最多允许存储的数据元素个数）为MaxSize，则元素位置为 0 至MaxSize-1，栈如图 1-7 所示。

  • 栈顶

    允许插入与删除的一端，通常用top表示。

  • 栈底

    不允许插入与删除的另一端，通常用bot表示。

QQ截图20240913154106

栈的运算

（1）入栈（PUSH）
在栈顶插入元素，也称进栈。
①若top≥MaxSize-1 时，则给出溢出信息，作出错处理。即进栈前首先检查栈是否已满，满则溢出；不满则进行②操作。
②置top=top+1；即栈指针加 1，指向进栈地址。③Stack[top]=X；即X为新进栈的元素。
（2）退栈（POP）
删除栈顶元素，也称出栈。
①若top≤-1，则给出下溢信息，作出错处理。即退栈前先检查是否已为空栈， 空则下溢；不空则进行②操作。
②X=Stack[top]，即退栈后的元素赋给X。
③top=top-1，即栈指针减 1，指向新的栈顶。
（3）读元素（GET）
将栈顶元素赋给一个指定的变量，也称取元素，此时top指针无变化。
①若top≤-1，则给出下溢信息，作出错处理。即退栈前先检查是否已为空栈， 空则下溢；不空则进行下一步操作。
②X=Stack[top]，即退栈后的元素赋给X。

栈的特征

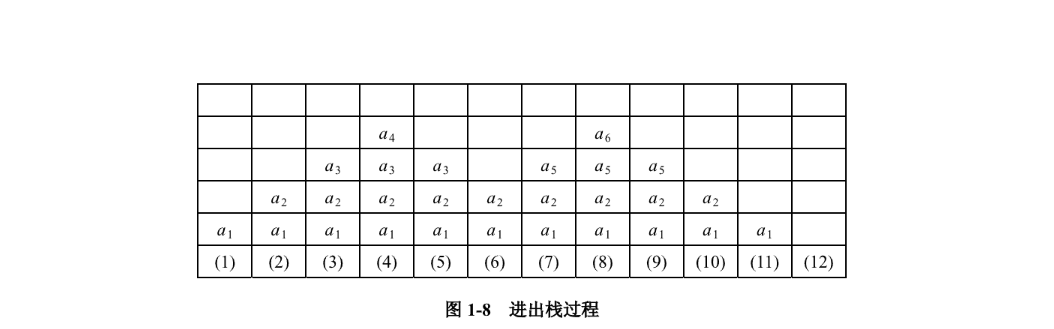
栈顶元素总是最后被插入的元素，栈底元素总是最先被插入的元素，即先进后出或后进先出。如(1)a1、(2)a2、(3)a3、(4)a4依次进栈，其次(5)a3、(6)a4出栈，然后(7)a5、(8)a6依次进栈，最后(9)-(12)所有元素出栈的过程如图 1-8 所示。

队列的概念

队列是指允许在一端（队尾）插入，而在另一端（队头）进行删除线性表，如图1-9所示

  • 队尾指针（rear）

    指向队尾元素。

  • 队头指针（front）

    指向排头元素a3的前一个位置

  • 空队列与满队列

    对于普通队列，射其空间大小为Maxsize。当rear=front时，为空队列；当rear=Maxsize-1时，为满队列。

队列的运算

（1）入队（EnQueue）从队尾插入一个元素。
①若rear = MaxSize-1 时，则给出溢出信息；否则进行②操作。②置rear = rear +1；即队尾指针加 1，指向入队地址。
③ ； Queue [rear]=X 即X为新入队的元素。
（2）出队（DeQueue）从队头删除一个元素。
①若rear = front时，则给出溢出信息；否则进行②操作。
②置front = front +1；即队头指针加 1，指向出队地址。③ ； X = Queue [front] 即X为出队的元素。

队列的特征

队列是先进先出或后进后出的线性表。如a1、a2、a3、a4依次入队，其次出队 2 个元素，然后a5、a6入队，最后所有元素全部出队的过程如图 1-10 所示。

循环队列

  • 假溢出

    若用MaxSize为 6 的顺序表实现图 10 的入出队操作，运算结束后，rear = front且rear = MaxSize-1。rear = MaxSize-1 表示队满，即此时已不能进行入队操作，否则将溢出；但实际上，这是一个空队列。这种现象称为假溢出，可用循环队列解决该问题。

  • 循环队列的概念

    循环队列是在逻辑上将队列存储空间的最后一个位置作为第一个位置的前一个位置，形成环状空间。MaxSize为 8 的循环队列如图 1-11 所示。

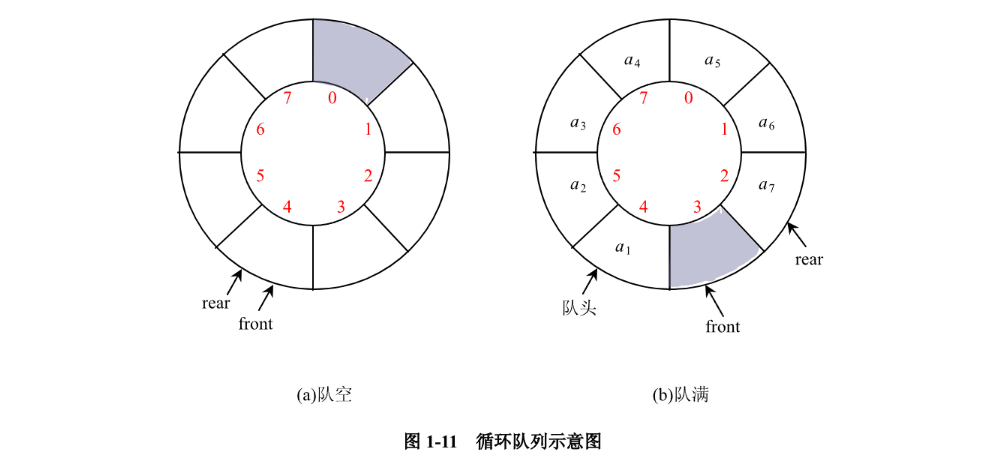
    循环队列最多只能存储Maxsize-1个元素

    • 空循环队列：队列的条件仍是front=rear
    • 满循环队列：队满的条件为front=（rear+1）%Maxsize。
    • 循环队列中的元素的个数n:若rear>=front,则n=rear-front;否则n=Maxsize+rear-front.
    • 循环队列中空余存储位置数m：m=(Maxsize-1)-n.

  • 循环队列的运算

    ①入队（EnQueue）
    (a)若front=(rear+1)%MaxSize时，则给出溢出信息；否则进行②操作。(b)置rear = (rear +1) %MaxSize；即队尾指针加 1，指向入队地址。
    (c)Queue [rear]=X；即X为新入队的元素。
    ②出队（DeQueue）
    3
    (a)若rear = front时，则给出溢出信息；否则进行②操作。
    (b)置front = (front +1) %MaxSize；即队头指针加 1，指向出队地址。(c)X = Queue [front]；即X为出队的元素。
    ③取队头元素（GetHead）
    (a)若rear = front时，则给出溢出信息；否则进行②操作。
    (b)X = Queue [(front +1) %MaxSize]；即X为队头的元素；此时队头元素不出队。

树与二叉树

树的基本概念

树是一种数据元素之间的关系具有明显的层次特点的非线性结构，每个结点最多只有一个前趋结点，可能没有或者有一个或多个后继结点，如图

（1）父结点
某结点的前趋结点称为父结点，又称双亲节点。如图 1-12 中，A是B的父结点，也是C和D的父结点；B是E和F的父结点。
（2）根结点
只有一个结点没有前趋结点，该结点称为树的根结点，简称树的根，如图 1-12 中的A。通常用根结点表示对应的树，如图 1-12 中的树称为树A。
（3）子结点
某结点的后继结点称为子结点，也称为子树或孩子。如B是A的子结点， C和D也是A的子结点；E和F是B的子结点。

（4）叶子结点
没有后继结点的结点称为叶子结点，如C、E、G、H、I、J和L都是叶子结点。

（5）结点的度
一个结点所拥有的后继结点的个数称为该结点的度。如图 1-12 中，A的度为 3，B的度为 2，C的度为 0。

（6）树的度
树的所有结点中最大的度称为树的度。如图 1-12 中，D的度为 4，是树中结点度的最大值，所以树A的度为 4。

（7）树的深度
树中结点的层次从根开始向后依次计算，根为第 1 层，根的子结点为第 2 层，根的子结点的子结点为第 3 层，以此类推。树的最大层次称为树的深度，如树A的深度为 5。

二叉树的基本概念

二叉树是一种特殊的有序树。
（1）二叉树的定义
二叉树是一棵空树；或者是一棵由一个根节点和两棵互不相交的，分别称作左子树和右子树的二叉树组成的非空树。
二叉树结点的度可以为 0（叶结点）、1（只有一棵子树）或 2（有 2 棵子树）。
（2）二叉树的基本形态
二叉树有 5 种基本形态，如图 1-13 所示。

几种特殊的二叉树

（1）斜树
①左斜树：只有左子树的二叉树。
②右斜树：只有右子树的二叉树。斜树是深度最大的二叉树。

（2）满二叉树
除最后一层外，其他每一层上的所有结点都有两个子结点。满二叉树是结点最多的二叉树。
（3）完全二叉树
除最后一层外，其他各层上的结点数均达到最大值；最后一层只缺少右边的若干结点。图 1-16(b)中，从右到左依次去掉N、M、L、K、J、I、H、G…，得到的都是完全二叉树。
①对二叉树从上到下、从左到右连续编号，完全二叉树中的结点编号与满二叉树相同。②完全二叉树中，度为 1 的结点的个数为 0 或 1。

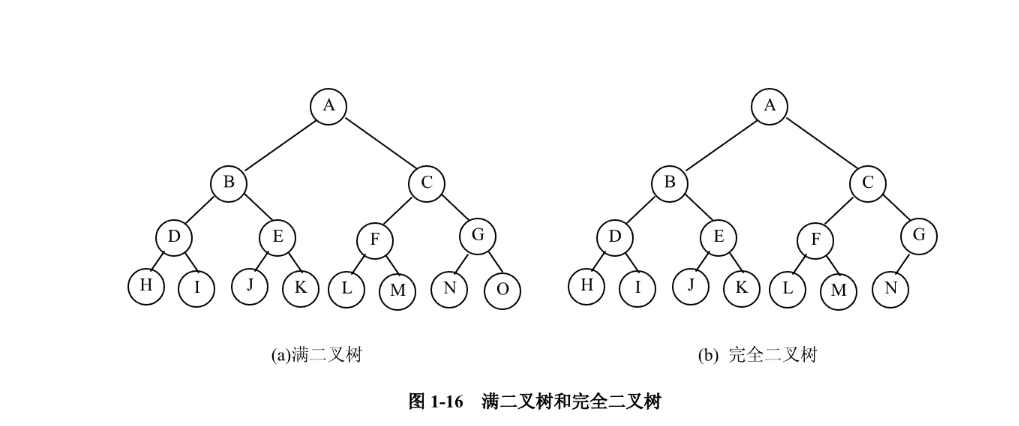
满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树；完全二叉树是深度最小的二叉树；二叉树通常采用链式存储结构，用两个指针域分别表示左右子树；满二叉树和完全二叉树可以按层序（从上到下、从左到右）采用顺序存储。

（4）堆
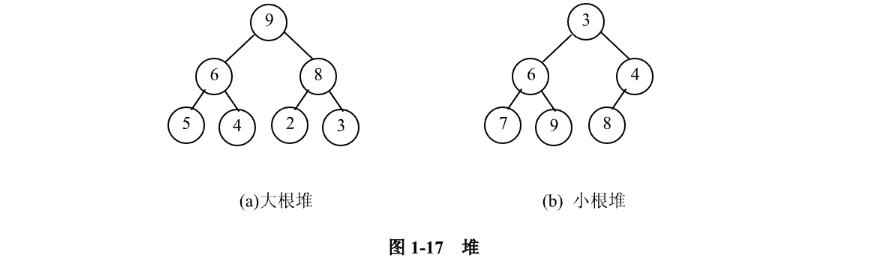
堆是一棵顺序存储的完全二叉树，堆中某个节点的值总是不大于或不小于其父节点的值，如图 1-17 所示。
①大根堆：ki >= k2i且ki >= k2i+1
②小根堆：ki <= k2i且ki <= k2i+1

二叉树的基本性质

性质1 在二叉树的第k层上，最多有 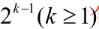个结点。

性质2 深度为n的二叉树最多有 2ⁿ-1个结点。

性质3 在任意一棵二叉树中，度数为 0 的结点（即叶子结点）个数n0总比度为 2 的结点个数n2大 1，即n0=n2+1。

性质4 具有n个结点的完全二叉树深度为 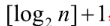，其中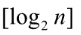表示取的整数部分。

性质5 设完全二叉树共有n个结点，如果从根结点开始，按层序（每一层从左到右）用自然数 1、2、…、n给结点进行编号，则对于编号为k（k=1，2，…，n）的结点有以下结论：
①若k=1，则该结点为根结点，它没有父结点；若k>1，则该结点的父结点的编号为[k/2]。②若 2k≤n，则编号为k的结点的左孩子编号为 2k；否则该结点无左孩子（显然也没有右孩子）。
③若 2k+1≤n，则编号为k的结点的右孩子编号为 2k+1；否则该结点无右孩子。

二叉树的遍历

二叉树的遍历是指不重复地访问二叉树中的所有结点，有以下三种方法。
（1）前序遍历（DLR）
若二叉树为空，则结束返回；否则首先访问根结点，然后遍历左子树，最后遍历右子树；并且遍历左右子树时，仍然采用前序遍历。前序遍历又称先序遍历。
（2）中序遍历（LDR）
若二叉树为空，则结束返回；否则首先遍历左子树，然后访问根结点，最后遍历右子树；并且遍历左右子树时，仍然采用中序遍历。
（3）后序遍历（LRD）
若二叉树为空，则结束返回；否则首先遍历左子树，然后遍历右子树，最后访问根结点；并且遍历左右子树时，仍然采用后序遍历。
对于图 1-18 所示的二叉树，其前序遍历结果为ABDECFG，中序遍历结果为DBEACGF，后序遍历结果为DEBGFCA。